In questo esercizio, partendo dal valore degli angoli dei cateti e dall’ipotenusa riusciremo a trovare il valore dei cateti e degli angoli la cui misura ci manca, sfruttando i teoremi sugli angoli dei triangoli rettangoli.
Testo dell’esercizio d’esempio
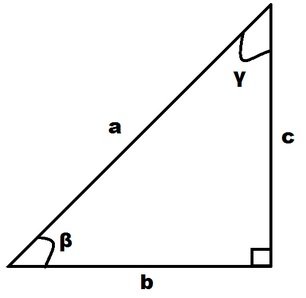
Nominiamo con la lettera a il valore della misura dell’ipotenusa di un triangolo rettangolo (riportato nella figura qui sopra), dove b e c saranno invece i valori dei cateti; β e γ saranno invece rispettivamente le ampiezze degli angoli opposti al cateto b e al cateto c.
Trovare le misure relative ai cateti sapendo che:
-
1) a = 10
-
2) β = π/6
Soluzione dell’esercizio
Applichiamo per risolvere questo esercizio il seguente teorema:
“In un triangolo rettangolo la misura di un cateto è uguale a quella dell’ipotenusa moltiplicata per il coseno dell’angolo acuto a esso adiacente oppure per il seno dell’angolo opposto.“
Pertanto sarà:
c = a x cosβ = 10 x cos π/6 = 10 x V3/V2 = 8,66
Quindi c = 8,66
Inoltre γ = 180 – (90 + 30) = 60 gradi
Ora non ci resta che applicare il teorema di pitagora per trovare b:
a” = b” + c”
100 = 75 + c”
25 = c”
c = 5
Vai all’esercizio successivo >>>