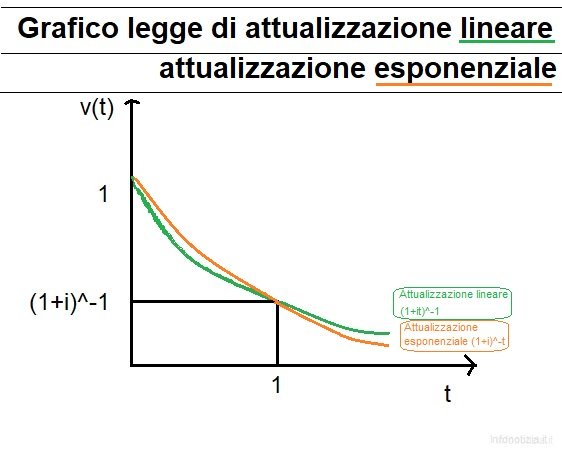
Spiegazione del grafico riguardante la legge esponenziale e la legge lineare di attualizzazione
Nell’ambito di un’operazione di attualizzazione, da svolgersi nel tempo t superiore o pari a zero, dobbiamo prendere in considerazione i due regimi distinti, lineare ed esponenziale. Il primo regime, il regime lineare, presenta un fattore di attualizzazione che segue la legge v(t) = (1+it)^-t; la legge esponenziale invece presenta il fattore di attualizzazione secondo la legge esponenziale v(t) = (1+i)^-t.
A questo punto viene spontaneo chiedersi quale regime di attualizzazione convenga usare.
Quando usare il regime di attualizzazione lineare e quando usare il regime di attualizzazione esponenziale?
Osservando i grafici (approssimativi) ci accorgiamo che nell’arco di un’attualizzazione che si svolga con tempo minore di 1, quindi di breve durata, ci converrà attualizzare tramite interessi composti, mentre per operazioni di attualizzazione di lunga durata, quindi superiori all’anno, ci converrà utilizzare gli interessi semplici.
Alla durata di un anno precisa i due regimi di attualizzazione restituiscono il medesimo valore.
Approfondimenti consigliati