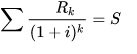L’azienda per cui siete consulenti finanziari ha ricevuto nella giornata di oggi un prestito di importo pari a 10000€, che di conseguenza dovrà essere restituito, tramite una rata da versare fra 3 anni pari a 9000 e una rata da versare fra 6 anni pari a 2800 euro. Vi giunge la richiesta di consulenza per trovare il tasso annuo d’interesse a cui rendere possibile l’ammortamento del debito.
Procediamo dunque alla soluzione dell’esercizio ponendo in atto la condizione di chiusura finanziaria o di equità, quindi la regola secondo cui sommando i valori attuali delle singole rate si debba eguagliare il capitale prestato totale.
In formule potremo scrivere:
Sostituendo alla formula i nostri dati del problema otteniamo:
10000 = 9000/[(1+i)^3] + 2800/[(1+i)^6]
Ponendo che sia x = (1+i)^-3 possiamo sostituire le incognite in questa maniera:
10000 = 9000 * [x] + 2800*[(x^2)]
Riscriviamo in maniera più pulita questa equazione di secondo grado:
10 = 9x + 2,8*(x^2)
2.8 x^2 + 9x – 10 = 0
Risolvendo questa semplice equazione di secondo grado otterremo
x = 0,873651
Da cui, sostituendo (1+i)^-3 con x otterremo:
(1+i)^-3 = 0,873651
a seguire:
1/(1+i)^3 = 0,873651
1= 0,873651*(1+i)^3
1,14462 = (1+i)^3
1,046053 = 1 + i
i = 0,046053
Approfondimenti consigliati: