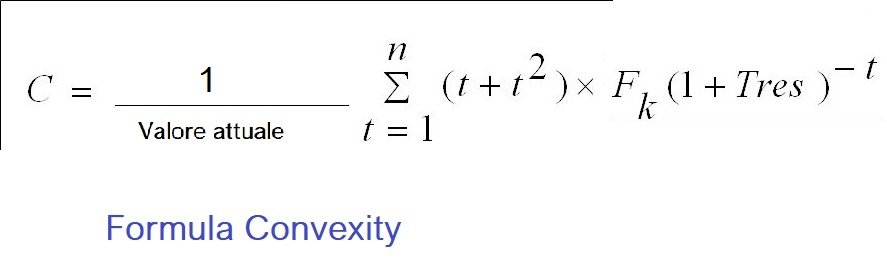La formula della Convexity
Qui di sopra è riportata la formula da utilizzare per il calcolo della Convexity di una rendita, continuando a leggere potrai anche osservare un esempio di calcolo della Convexity nel caso di una rendita su base annuale.
Testo dell’esercizio d’esempio per il calcolo della convexity
Poniamo l’esistenza di una rendita A avente tasso Tres pari a i = 0,08 avente i valori di Rt e periodi di tempo t riportati di sotto; si proceda al calcolo della convexity di Macaulay.
Ra/tempo -> (3000, 4000) / (2 anni/30anni)
Soluzione dell’esercizio di matematica finanziaria sulla convexity
Per prima cosa calcoliamo il valore attuale della rendita:
V1: 3000/(1,08^2) = 3000/1,1664 = 2572,016
V2: 4000/(1.08^30) = 4000/10,063 = 397,50
Quindi il valore attuale della rendita sarà 2572,016 + 397,50 = 2969,51 €
Continuiamo quindi effettuando il calcolo della convexity:
1/2969,51 *{[(2^2 + 2)*3000/(1.08^2)] + [(30^2+30)*4000/(1.08^30)]}
1/2969,51 *{[(6)*3000/(1.1664)] + [(930)*4000/(10.06265)]}
1/2969,51 *{[(18000/(1.1664)] + [3720000/(10.06265)]}
1/2969,51 *{[15432.098] + [369683,9302]}
Convexity = 129.69
Cos’è la Convexity?
La matematica finanziaria definisce la convexity di Macaulay come il grado della curvatura della funzone prezzo; oltre alla formula riportata di sopra è possibile ottenere la curvatura (quindi calcolare la convexity) anche facendo il rapporto tra la derivata seconda, che deve essere calcolata a fronte delle variazioni del tasso di interesse) e la stessa funzione.
A cosa serve la convexity?
L’utilità della convexity come indice è quella di fornire un rendiconto riguardanti gli aspetti della funzione prezzo: viene quindi utilizzata per costruire l’approssimazione della funzione tramite una parabola; può essere utilizzata anche come indice del rischio di un titolo.