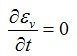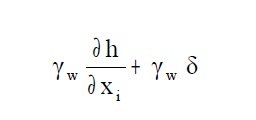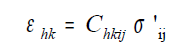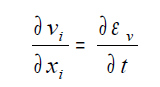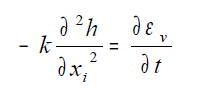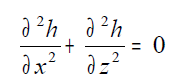Geotecnica: modellazione di un banco di terreno ed equazioni di moto

Si schematizza il banco di terreno come un mezzo poroso continuo bifase saturo ed effettuando le ipotesi di fluido incomprimibile e scheletro solido indeformabile; in cui le due fasi sono supposte sovrapposte e mutuamente interagenti.

Regime stazionario

Operando in regime stazionario si ha che le variazioni di volume nell’unità di tempo sono nulle, per cui si può scrivere:

Equazioni di equilibrio per lo scheletro solido

Le azioni scambiate con il contorno sono di tipo normale e tangenziale, mentre come forza di massa si considera la sola forza peso. Si scrive l’equazione di equilibrio in forma indiciale in termini di tensioni efficaci: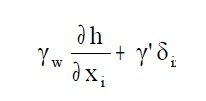

Equazioni di equilibrio per il continuo liquido

Effettuando la differenza tra il sistema di equazioni indefinite dell’equilibrio scritto in termini di tensioni totali ed efficaci si ricava l’equazione di equilibrio in forma indiciale per il continuo liquido:

Equazioni di congruenza

Le deformazioni, definite dal tensore, devono essere congruenti con il campo di spostamenti per cui non possono aversi distacchi o compenetrazioni di materia. Si scrivono delle semplici relazioni geometriche tra deformazioni e spostamenti.

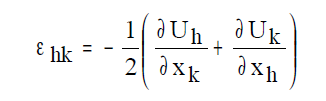
Legame costitutivo

Le equazioni che regolano il comportamento di uno specifico materiale sono le relazioni esistenti tra azioni e deformazioni. In quest’ambito per semplicità, si ipotizza legame di tipo elastico-lineare, in modo tale che il tensore che mette in relazione tensioni e deformazioni risulti essere composto da elementi costanti:

La matrice [6 x 6] è detta tensore di cedevolezza e tutti i suoi termini per l’ipotesi di mezzo isotropo dipendono solo da due costanti, il modulo di Young E e il coefficiente di Poisson υ.

Equazione di compatibilità idraulica

Nelle ipotesi fatte di liquido incomprimibile e scheletro solido indeformabile, l’equazione di compatibilità idraulica rappresenta un bilancio tra la portata di acqua espulsa e la variazione di volume nell’unità di tempo. Per tener conto dell’interazione tra i due materiali che costituiscono il nostro mezzo, ossia fluido e scheletro solido, nell’ipotesi di particelle e fluido incomprimibile, ma scorrimento relativo consentito, ad una variazione della velocità di filtrazione del fluido nel mezzo poroso lungo una generica direzione corrisponde una variazione di volume nel tempo, ossia: