Premesso che sia ABC un triangolo qualunque partiamo dall’enunciato che vogliamo dimostrare:
<< In un triangolo qualunque la misura di un lato è uguale alla somma dei prodotti delle misure degli altri due lati per il coseno dell’angolo che ciascuno di essi forma col primo. >>
Come dimostrare il teorema delle proiezioni
Vogliamo dimostrare che:
BC = AC x cos γ + BA cos β
Sia nel caso in cui sia β che γ siano angoli acuti quanto nel caso in cui uno di essi sia ottuso.
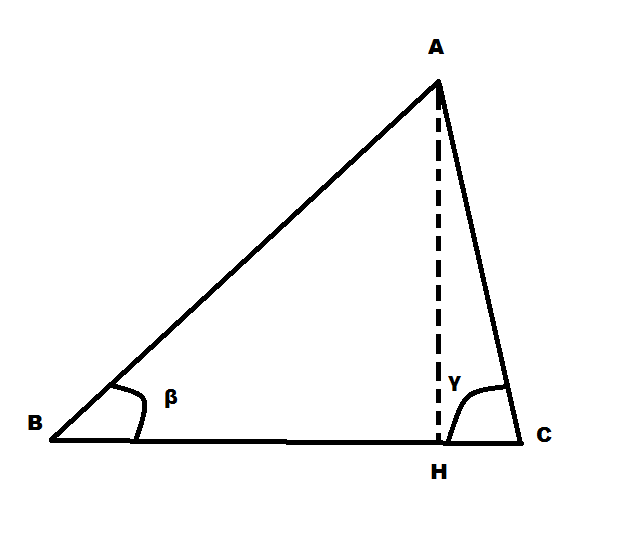
Esaminiamo ora il caso in cui 0 < β < π/2 e sia 0 < γ < π/2
La perpendicolare condotta dal vertice A alla retta del lato BC incontra la retta stessa in un punto H interno a BC. Essendo: BC = BH + HC allora applicando il teorema dei triangoli rettangoli ai triangoli ABH e AHC si otterrà:
BH = Ba x cos β
HC = AC x cos γ
Sostituendo a BC = BH + HC otteniamo:
BC = AC x cos γ + BA cos β
E abbiamo dimostrato il teorema.
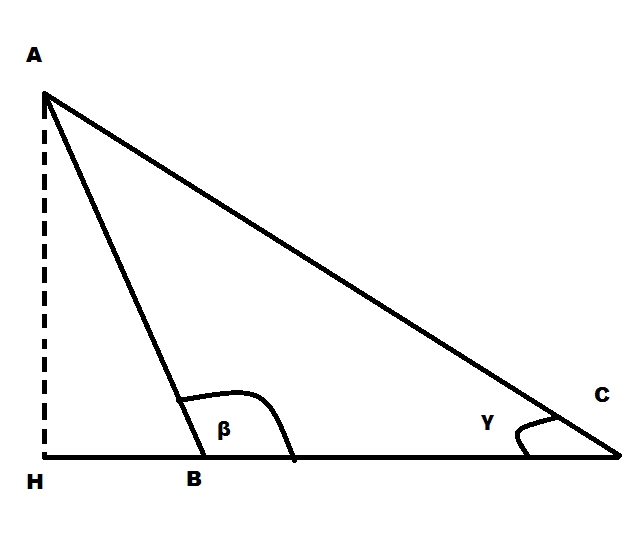
Nel secondo caso in cui sia invece π/2< β < π
La perpendicolare condotta dal vertice A alla retta del lato BC incontra la retta stessa in un punto H esterno a BC.
Essendo: BC = HC – HB
Essendo l’angolo ABH = π – β
Applichiamo il teorema dei triangoli rettangoli ai triangoli AHB e AHB ottenendo:
HC = AC cos γ
HB = AB cos (π – β) = AB (cos π cos β + sen π sen β) = AB[(-1 x cos β) + (0 x senβ)] = – AB cos β
Pertanto, sostituendo alla precendente ugualianza otteniamo: BC = AC x cos γ + BA cos β