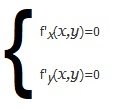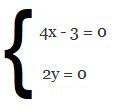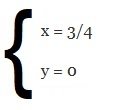Introduzione
I problemi di ottimizzazione libera sono di solito utilizzati per ricavare i parametri utili a raggiungere il rendimento massimo o il minimo rapporto tra parametri.
Esercizio d’esempio
Partiamo subito da questo problema di ottimizzazione libera: trovare il massimo e il minimo assoluti della funzione a due variabili f(x.y): 2x^2 + y^2 – 3x
Soluzione dell’esercizio con il metodo dell’Hessiano
Anzitutto dovremo ricavare le derivate parziali prime della funzione:
- Derivando in x: f’x(x,y)= 4x – 3
- Derivando in y: f’y(x,y)= y
Adesso sarà il momento di risolvere il sistema formato da f’x(x,y)=0 e f’y(x,y)=0 (condizione necessaria):
Ossia, sostituendo le derivate parziali prime avremo che 4x – 3 = 0 e 2y = 0 :
Quindi avremo che x = 3/4 e y = 0:
Pertanto il punto (3/4 , 0) è un punto stazionario.
Sarà pertanto un punto di massimo o di minimo oppure un punto di sella.
Adesso calcoliamo le derivate parziali seconde:
- f”xx(x,y) = 4
- f”xy(x,y) = 0
- f”yx(x,y) = 0
- f”yy(x,y) = 2
Si calcola poi usando la matrice Hessiana il determinante (Hessiano) e si sostituiscono le coordinate dei punti trovati nel risultato trovato.
Se il determinante della matrice Hessiana è > 0 allora abbiamo 2 casi:
- Se f”xx > 0 allora avremo un minimo
- Se f”xx < 0 allora avremo un massimo
Infine se il determinante della matrice Hessiana è <0 allora avremo un punto di sella.
Nel nostro caso il determinante della matrice è = (4 x 2) – 0 = 8: quindi è > 0
f”xx = 8, con 8> 0.
Pertanto avremo nel punto (3/4,0) un punto di minimo.